Anamorphic images are distorted images.
You all know the fun children have in museums or at fairs when they
see themselves distorted in big concave or convex mirrors. There are
many types of anamorphic images. Only two of these will be described
here.

Here are some distorted words in Latin
letters (made with CORELDRAW). Try to recognize what is written here.
It is possible but not clear at the first look. However, if you view
this image at a very shallow angle, you will recognize it. The first
view reveals 'ICPE 2000' at the bottom; then the view perpendicular
to the first view reveals anamorphic. This type of simple perspective
anamorphic distortion can be found in many places: in paintings, wall
paintings, drawings, underground stations or on the streets. This
type of anamorphosis was closely related with the development of perspective
in the fifteenth and sixteenth centuries. And of course you can describe
this in mathematical terms as a relatively simple form of linear transformations.
The so-called cylindrical anamorphoses
were not developed until quite a time later. The pictures appear correct
when observed with a cylindrical mirror. Mainly artists used this
form of anamorphic pictures, not only in Europe but also in Chinese
culture, and they used it without thinking in physics or mathematical
terms. With anamorphic images you can hide the content. If you know
the trick of how to resolve the image, you can see them normally.
Therefore these images have a certain magic aspect. And this is fascinating
not only for children, but for adults as well.
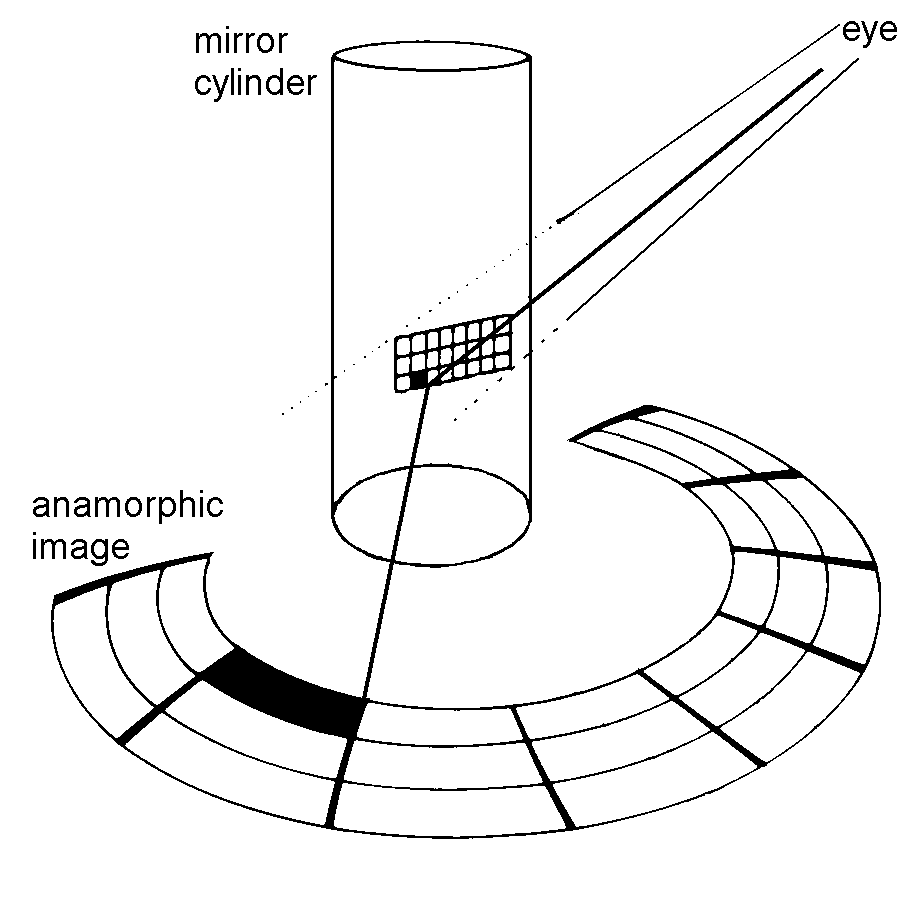
Here is a drawing which shows the basic
construction of anamorphic grids. The observer is at a finite distance
from the cylindrical mirror. One reflected ray is drawn in a thick
line. The construction uses only the law of reflection, which means
that the angle between the incident ray and the perpendicular ray
to the cylinder surface must be the same as the angle between the
perpendicular and the reflected ray.
With a computer you can develop new formulas
to calculate any anamorphic picture pixel by pixel.
One method of calculating anamorphic
images is the so-called raytracing. In raytracing anamorphic images,
a virtual slide projector with the non-distorted, original image is
assumed. From the eye a ray goes through the original image pixel
by pixel and hits the mirror, where it is reflected and then hits
the plane or another surface in a pixel. The color of the pixel is
the same as in the image.
The German student Friedel Ulrich developed
a program for anamorphic images with the raytracing method as a thesis
in college at the German Gymnasium in Pfaffenhofen, Bavaria. The structure
of his program is simple: a camera, a mirror object (cylinder, cone
or sphere) and a plane can be selected and positioned. A digitalized
image, e.g. from a digital camera, can be inserted. The program calculates
the anamorphic image. The file ANAMORPHUENGLISH.ZIP with the program
ANAENGL.EXE and a short help-file can be downloaded from the internet
(URL:http://www.e20.physik.tumuenchen.de/~cucke/ftp/anamorph/ulrich/anamorphuenglish).
With a Pentium 400MHz processor you need several minutes to calculate
the anamorphic picture.

This example - a cylindrical anamorphosis
- was calculated with this program. I have to mention that anamorphic
images are normally turned upside down, which makes it even more difficult
to recognize the content. Take a cylindrical mirror (easily available
from chromatized syphon tubes, bended reflecting mirror foils or other
sources) and view the anamorphic image. Perhaps you will have to enlarge
the image with a copy machine.
Make your own very special greeting card
for the next millennium either as a linear or as a cylindrical anamorphic
image.


