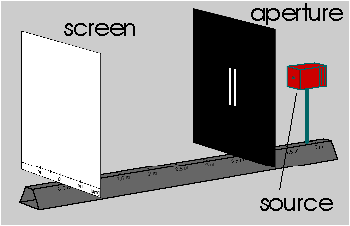
Please install the program now by executing the file "Doppelspalt_V31.exe". If you are not in posession of this file, you can download it here.

Now take some time to test and explore the program. You can switch on
the source in the control panel on the right side (or simply by clicking
on the support rod of the source).
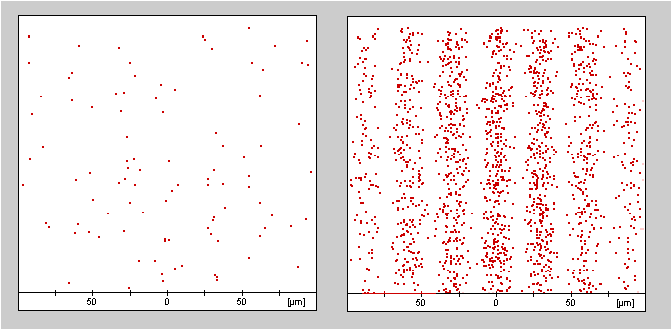
![]() Turn
off the source and look at the pattern that the electrons formed on the
screen. Suppose you were to send in a single electron through the slits.
Can you predict at which position on the screen the electron will be detected?
Turn
off the source and look at the pattern that the electrons formed on the
screen. Suppose you were to send in a single electron through the slits.
Can you predict at which position on the screen the electron will be detected?
Perform the experiment by switching on the source for a short time. A new spot appears on the screen and it was not likely that you predicted its exact location.
![]() The
prediction becomes more successful if we modify the experiment a little.
Now, 100 electrons are to be added. You can probably predict with a good
accuracy at which places it is likely to find many electrons and at which
positions only few are found.
The
prediction becomes more successful if we modify the experiment a little.
Now, 100 electrons are to be added. You can probably predict with a good
accuracy at which places it is likely to find many electrons and at which
positions only few are found.
The difference between the two experiments lies in the fact that in the second experiment we changed the rules of the game. Instead of making a prediction about a single event, we made a probability statement. In fact, the success of quantum mechanics has its basis in its statistical predictions. In quantum mechanics, there is no means of predicting the results of single events (except for the trivial cases where the probability is zero or unity).
The statistical aspects of quantum mechanics are discussed in more detail in the following lesson. It is useful to lay some conceptual foundations first.
In general, physical objects that are to be analyzed in an experiment
must be brought into a definite state by the experimenter. They need to
have well-defined initial conditions, which are produced in the process
we call preparation.
Example: To get used to the terminology of preparation, interaction and measurement we consider a simple example from classical physics. On an air track table, we study the collision of two gliders in order to
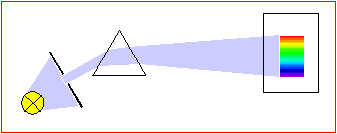
One supposes that light of a specific color possesses a certain property, because it deflected by a well-defined angle a through the prism. This idea can be tested as follows:
![]() Experiment
2: The light beam created in the first experiment is passed through
a second prism (figure below). Doing this experiment reveals that the light
beam is not spread out again by the second prism as the original white
light beam was spread into a spectrum by the first prism. As we conjectured,
it is deflected by just the same angle a
as the selected light
in the first prism.
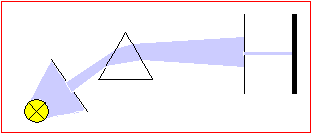
Experiment
2: The light beam created in the first experiment is passed through
a second prism (figure below). Doing this experiment reveals that the light
beam is not spread out again by the second prism as the original white
light beam was spread into a spectrum by the first prism. As we conjectured,
it is deflected by just the same angle a
as the selected light
in the first prism.
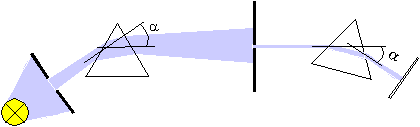
Light with these properties is produced by preparation. In this
case, the preparation is carried out by traversing the prism and the second
slit. Generally, physical systems with definite properties are brought
about by an act of preparation.
This scheme, comprising the preparation and test stages can be employed in a variety of physical situations. First one tries to prepare a certain property (e. g. wavelength, kinetic energy) on a physical object (e. g. light, electron). To make sure that the object really possesses this property, a second (possibly identical) experiment is performed that checks for this property.
If one can predict with certainty that a test yields a certain property in all cases you are allowed to ascribe this property to the physical object. In this case (and only in this case) the object really posseses this property. We will see later that one really needs to pay attention to this prescription. Later we will look at cases where contradictions arise with observed phenomena if we ascribe properties to quantum objects independent of a preparation or a test.
![]() Not
always is a dynamical property produced in an experiment.
Not
always is a dynamical property produced in an experiment.
This observation led us in Section 2 to consider probabilities. A complete preparation leads to reproducible predictions about the probabilities of events. In the double-slit experiment, the source prepares electrons with definite kinetic energy, thus they possess the property "kinetic energy". This preparation determines the probability distribution on the screen given the separation and the widths of the slits. We have been able to reliably predict the places where many electrons and where few electrons will be detected.
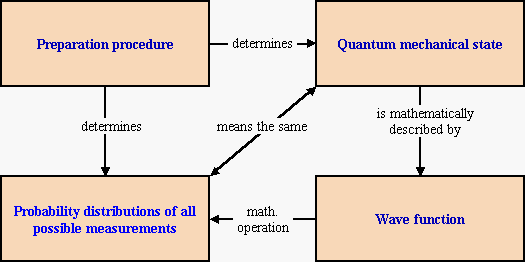
The preparation is independent of the subsequent interaction and measurement. We could for example perform a scattering experiment with the above electrons, and measure the distribution of scattering angles after the scattering. Therefore the preparation has to determine the probabilities for all possible experiments that can be performed on the prepared object. To make this connection between preparation and measured probability distributions more explicit, one introduces the notion of the quantum mechanical state. It is identified with the specification of a probability distribution for each possible measurement.
Mathematically, the quantum mechanical state is described by a wave function. With certain mathematical operations, it is possible to extract from the wave function the probabilities of all conceivable experiments. Quantitative statements then become possible. The conceptual connection between preparation, state, wave function and probability distribution is illustrated in the graphics below.
![]() For
future reference: Basis page on preparation
For
future reference: Basis page on preparation
Do you have comments or questions? Send an e-mail to the discussion
group: ![]()
[2] L. Ballentine, Quantum Mechanics. A Modern Development, World Scientific,
Singapore 1998.
Ballentine is one of the most prominent advocates of
the ensemble interpretation of quantum mechanics. In his book, therefore,
preparation and measurement are clearly distinguished. The quantum mechanical
state concept is clearly discussed. Section 5 of the present lesson rests
mainly on Ballentine`s Chapter 2.1.
[3] Kansas State University Physics Education Group (D. Zollman et al.),
Visual Quantum Mechanics, Manhattan, Kansas, 1998.
The Visual Quantum Mechanics Project pursued at the Kansas
State University provides hands-on materials for introducing quantum mechanics
on a qualitative level. The working sheet and Section 2 rest on these materials.
[4] R. Müller, H. Wiesner, Das Münchener Unterrichtskonzept
zur Quantenmechanik, Manuskript, 1999.
The material developed at the University of Munich is
an introduction to quantum mechanics that stresses mainly the conceptual
foundations. If not mentioned otherwise, the present lesson is based on
Chapter 2 of this manuscript.