- Spreadsheet Solutions
-
- In the exploration, the computer had already been programmed
to solve the equation. However, computers generally deal with
numbers, so we needed to convert the time dependent Schrödinger’s
Equation,
-
| |
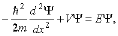 |
(1) |
- Into something a computer can work with. So, we approximate
a derivative as a different, or
| |
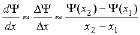 |
(2) |
- How well this approximation works depends on how rapidly
Y(x) is changing and how close x2 is to x1. For a second derivative
we repeat the process in equation (2). The end result is that
Y(x) at one value of x can be appropriately terms of its value
at other values of x. Many methods have been developed to make
the numerical solutions accurate and computationally fast. Our
purpose is to understand the principles, not the details of the
various methods. So we limit ourselves to a simple method called
Euler’s Method. In this method we determine the value of
Y(x) by extrapolating for its value at a previous location. The
basic scheme is summarized in Figure 1.
-

