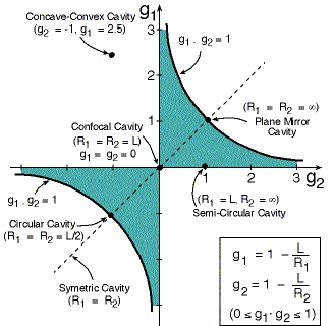
Figure 4.13: Stability Diagram of all laser cavities.
The stability criterion for laser cavity is:
In the stability diagram the geometric parameters of the mirrors are the axes x and y.
Figure 4.13 show the stability diagram of all laser cavities.

Figure 4.13: Stability Diagram of all laser cavities.
In the stability diagram, in figure 4.13, the dark region marks the area of stability.
The stability region is surrounded by two hyperbolas defined by the stability criterion.
A few common cavities are marked on the stability diagram.
A cavity is stable if the center of curvature of one of the mirrors, or the position of the mirror itself, but not both, are between the second mirror and its center of curvature.
Pay special attention for cavities on the edges of the stability region !
For these cavities, the product g1*g2 is either
"0" or "1".
An applet that
show how the stability diagram depends on the cavity parameters can be
reached by clicking
here Cavity Stability.
To check how the laser beam moves inside different type of cavities,
and how the cavity parameters determine the divergence of the beam, Click
here: Beams in Laser Cavity.