CHAPTER 2 SOLUTIONS TO PROBLEMS AND QUESTIONS

Citation: Jacqueline D. Spears and Dean Zollman, Instructor's Guide for The Fascination of Physics, (The Benjamin /Cummings Publishing Company, Inc., Menlo Park, CA 1985). Permission granted by the publisher.

Keywords: Textbook; Exposition; Mechanics; Kinematics; Motion; Introduction

A. Review Of Chapter Material

A1. The answers to the "A1" questions are found directly in the text. Look for each term printed in boldface type.

A2. Vectors: acceleration, velocity, average velocity, instantaneous velocity, acceleration due to gravity. Scalars: speed, average speed, instantaneous speed.

A3. A blur will indicate that motion occurred during the time that the picture was being taken. On a strobe photograph multiple images indicate that motion has occurred.

A4. By using speed and velocity we can compare objects' motions when the objects have moved different distances and/or times.

A5. Average speed is the total distance divided by the time taken for the whole trip, while instantaneous speed is the speed at any specified "instant" during the trip. Instantaneous speed must be estimated by measuring distances over very short time intervals. Instantaneous speeds provide us with a better description of an object's motion when the object is accelerating.

A6. An object accelerates if its velocity changes. Thus, an object accelerates if either its speed or direction changes.

A7. The unit (m/s)/s is a measure of the rate at which speed is changing. A number of (m/s)/s means that the magnitude of the velocity is changing by that amount each second.

A8. When an object experiences positive acceleration, the magnitude of its velocity (and its speed) increases. When the acceleration is negative, the object's magnitude of velocity (and speed) decreases.

A9. The acceleration due to gravity is the same for all objects which fall near the surface of the same planet. It changes when you change from one planet to another.

A10. (a) When the images are equal distances apart, the object moves the same distance during each time interval. This result indicates that the object is moving at a constant speed. (b) When images are spaced further and further apart, the object is moving a greater distance during each successive time interval. Thus, its speed is increasing. (c) When images are spaced closer and closer together, the object is slowing down. Accelerations are occurring in (b) and (c) but not in (a).

B. Using the Chapter Material

B1. (a) Average speed = distance/time = (6000 km)/(526 h) = 11.4 km/h (b) Average speed = distance/time = (6000 km)/(57 h) = 105.3 km/h (c) Average speed = (6000 km)/(5.5 h) = 1091 km/h

B2. Average speed = distance/time = (100 m)/(50 s) = 2 m/s. You cannot state the velocity because you do not know the direction (or directions) moved.

B3. Time = distance/average speed = (465 km)/(80 km/h) = 5.8 hours.

B4. For the images on the left side of the photograph, her instantaneous velocity is pointing to the right and upward. Between the third and fourth images the instantaneous velocity must point down and to the right. The vector describing her average velocity points from the first image to the last. Thus, it is parallel to the ice and points to the right.

B5. The ball moves 20 cm = 0.2 m in falling from A to B. To determine the time we count the number of images between A and B. This number is six. The time between successive images is given in the text as 0.033 seconds, so the total time it takes the ball to fall from A to B is 6 x .033 s = .198 s. The best estimate of the speed between these points = distance/time = (.2 m)/(.198 9) = 1.01 m/s. This instantaneous speed will occur halfway between A and B, so it happens at .099 seconds.

B6. (a) For the entire race the runner's speed is the total distance divided by the total time. Average speed = (100 m)/(14 s) = 7.14 m/s. (b) The best we can do with the information presented is to estimate the runner's instantaneous speed as the speed over the first 10 meters. This speed = distance/time = (10 m)/(2 s) = 5 m/s. This instantaneous speed occurs halfway during the time interval. The runner's instantaneous speed is 5 m/s 1 second after the race has begun. (c) The instantaneous speed over the first 10 meters is lower; so the runner must have speeded up during the race.

B7. (a) Average acceleration = change in speed/time = (12 m/s - 0 m/s)/s 9 = 2 (m/s)/s. This acceleration is considerably less than the acceleration due to gravity. (b) Average acceleration = change in speed/time = (30 m/s - 0 m/s)/20 s = 1.3 (m/s)/s. This is less than the acceleration due to gravity. (c) Average acceleration = change in speed/time = (56 m/s - 0 m/s)/4 s = 14 (m/s)/s. This acceleration is greater than the acceleration due to gravity.

B8. Baby's acceleration = change in speed/time = (1 m/s - 2 m/s)/5 s = -0.2 (m/s)/s.

B9. (a) The total distance traveled is five times the distance for one revolution = 5 x 100 m = 500 m. The average speed = 500 m/250 s = 2 m/s. (b) Because the path was several complete revolutions, your ending point was the same as your starting point. Thus, your displacement was zero. and your average velocity was zero. (c) You were constantly changing direction so your velocity was constantly changing. Thus, you were always accelerating.

B10. The distance between images of the ball are much greater than the distance between images of the club. We conclude that the ball is moving much more rapidly than the club.

C. Extensions to New Situations

C1. (a) For each of the values use the equation: average speed = distance/time. So, average speed = distance/time = 10 m/1 s= 10 m/s; average speed = distance/time = 10 m/2 s = 5 m/s; average speed = distance/time = 10 m/4 s = 2.5 m/s; average speed = distance/time = 10 m/8 s = 1.25 m/s. (b) average speed = distance/time = 1 m/2 s = .5 m/s; average speed = distance/time = 2 m/2 s = 1 m/s; average speed = distance/time = 4 m/2 s = 2 m/s; average speed = distance/time = 8 m/2 s = 4 m/s. (c) Distance = speed x time = 1.5 m/s x .5 s - .75 m; distance = speed x time = 1.5 m/s x 2 d = 3.0 m; distance = speed x time = 1.5 m/s x 6 s= 9.0 m; distance = speed x time = 1.5 m/s x 12 s = 18.0 m. (d) When the average speed doubles while the distance does not change, the time must decrease by one-half. If the average speed triples, the new time must be one-third of the original time. (e) If the time does not change and the average speed doubles, the new distance must be twice the old distance. If the time stays the same and the new speed is 12 times the old, then the new distance must be twelve times the old distance. (f) When the average speed does not change and the time doubles, the distance traveled doubles. When the time increases by five times, the distance increases by a factor of five also.

C2. (a) Average speed - distance/time = 400 km/5 h = 80 km/h. (b) Distance traveled = 50 km/h x 2 h = 100 km. The remaining distance is 400 km - 100 km = 300 km. (c) Any answer will be acceptable here. The idea is to let students bring out their preconceptions before they answer the question. Generally, students tend to estimate a lower speed than the one calculated later. (d) You need to travel 300 km in 3 h. (e) Average speed = distance/time = 300 km/3 h = 100 km/h. (f) This answer will depend on your reasons for your answer in part (d).

C3. (a) The acceleration on the ball as it travels upward is in the direction opposite to the way it is moving. So, the ball must slow down. The magnitude of its velocity decreases. (b) On the way down the acceleration and the ball's velocity are in the same direction. The magnitude of its velocity increases. (c) The acceleration due to gravity is a constant on earth. It does not change. (d) Right at the top of its flight the direction in which the ball is moving changes from up to down. Just before it changes direction, the ball has zero velocity. (e) As an object rises, its velocity decreases in magnitude until at the top of its path its velocity is zero. As the object falls, its velocity increases in magnitude until the object is stopped. During this time the acceleration is that due to gravity and never changes.

C4. (a) A car moving in heavy traffic will have frequent starts and stops. It will move relatively fast at some times and not at all at others. The average speed will be quite different than most of the instantaneous speeds. (b) As the ball travels to the batter the only acceleration is that due to gravity. This will cause a slight change in the ball's speed so the average speed will be slightly different than instantaneous speeds. (c) The answer this one depends on the runner's strategy for the race. Some runners will choose to maintain the same speed throughout the entire race. Their average and instantaneous speeds will be the same. Most runners, however, will attempt to maintain the same speed during most of the race but have a greater speed at the end. Thus, their instantaneous speed at the end could be very different from their average speed. (d) As the sun moves across the sky, it moves at a very constant rate. The instantaneous speed and average speed will be identical. (e) Many different speeds will be involved here- the ground speed of the airplane, its take-off speed and its cruising speed. The instantaneous speed at most times will be different from its average speed.

C5. The rearrangement of the equation gives change in velocity = acceleration x time,

and time = change in velocity acceleration

(a) time = (change in velocity)/acceleration = (39.2 m/s - 0 m/s)/9.8 (m/s)/s = 4 s. (b) Since the ball started with zero speed, its change in velocity will equal its final velocity. Change in velocity = 9.8 (m/s)/s x 10 s = 98 m/s.

C6. The ratio is useful because it allows us to compare specific quantities even though certain conditions may be different. In this chapter we could compare the speeds of two objects when each had traveled a different distance and a different time. Similar comparisons could be made for accelerations. A very useful ratio which we use in the grocery store in called the unit price. It tells us how much a specific amount (say one ounce) of an item costs. This quantity lets us determine if a 12 ounce can costing $1.95 is a better buy than a 10 ounce can at $1.69. Another useful ratio is the number of people per square mile living in an area.

C7. (a) The screwdriver is moving with the astronaut before she releases it. because she gives it no acceleration, she causes no chance in the velocity of the screwdriver. Thus, the screwdriver will continue to move with the velocity it had before it was released. Its velocity will be the same as the astronaut's. (b) Since the screwdriver is moving at the same velocity as the astronaut, it will remain next to her hand. [If these ideas seem a little confusing, be patient. We will learn more about them in the next few chapters.]

C8. (a) To answer this question we need to look at the distance between consecutive images as they move horizontally. The best way to do this is to draw lines down to the bottom of the picture and use the bottom as the horizontal axis, then compare distances between the lines. Doing this, we find that the lines are approximately equally spaced along the horizontal axis. We conclude that the speed in the horizontal direction does not change. (b) If we perform the same operation as in part (a) but use the left edge of the photograph as the vertical axis, we find that the distance between consecutive images gets closer together as the ball rises and further apart as the ball falls. We conclude that the ball is accelerating in the vertical direction.

(c)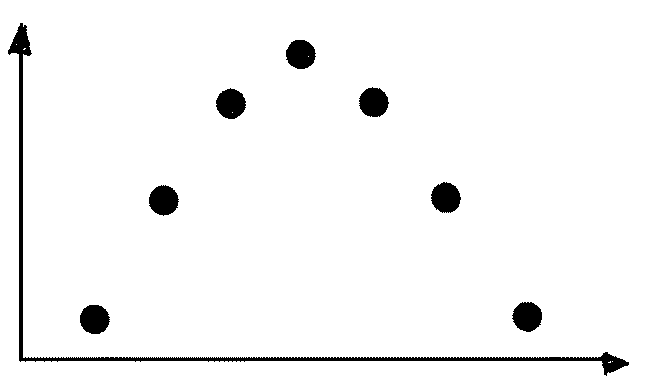

(d) See Figure

(e) The average speed and the average velocity will be quite different. The path of the motion is a relatively long arch while the displacement is a straight line along the bottom of the photograph. The times for the two quantities are equal. Thus, the magnitude of the velocity will be different from the speed. (f) Because the acceleration due to gravity on the moon is much less than that on earth, we should expect the change in speed to be less than on earth. The ball would slow down less rapidly and reach a greater height.

C9. A sprint lasts for only a short time. Thus, it is important that each runner gets to his/her maximum speed as quickly as possible and hold that speed for a short duration. Maximum possible acceleration is required. A long distance race, on the other hand, has a rather long duration. Runners need to maintain a constant pace but not at their maximum possible speed. They do not need to increase their speed as rapidly.

C10. (a) At the beginning of the swing the golf club increases its speed rather quickly. Then, at the bottom of the swing it is moving at a constant speed for a short distance before its speed decreases as it reaches the top of the swing. (b) The velocity of the club is continually changing because of the almost circular path of the golf club. In addition to this constant change, the magnitude of the club's velocity is also changing. This change in magnitude follows the same pattern as the changes in speed. (c) At the beginning of the swing the golf club is accelerated in the same direction as the club is moving. At the same time the club is turning in a circle so it is being accelerated toward the center of the almost circular path. The total acceleration is the combination of these two. At the end of the swing the acceleration toward the center of the circle is continuing. However, in addition the club is slowing down. So, an acceleration is in the opposite direction as the direction the club is moving. Again, the total acceleration is the combination of these two.