So far we have been thinking of wave functions in bound states as 1-dimensional standing waves, kind of like the vibrating string videos we looked at. We have used a number n (the quantum number) to describe the lowest to highest energy wave functions.
For example n = 1 corresponds to the first standing wave that has a node at each end and an anti-node in the middle.
The second, n = 2, has a node in the center.
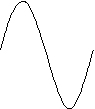
The third n = 3, has an anti-node in the center.
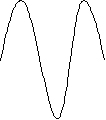
An atom is clearly a three-dimensional entity so we must spend some time thinking about what this means in terms of the wave functions of the electrons. The electron feels an attractive force from the nucleus. The potential energy goes as 1/r, where r is the distance from the nucleus.
For the electron:
Total Energy = Kinetic Energy + k x Qn x Qe/r
Qn is the charge on the nucleus, Qe is the charge on the electron and k is a constant.
It may be a little difficult to imagine this potential energy in three dimensions. We have been simplifying the 1/r potential to a square well. The three-dimensional form of a square well is a box. Not only can the electron move back and forth, it can also move in orbits.
Professor Daniel A. Russell of Kettering University produced
these animations and kindly allowed us to use them for this course.
To get a feel for what three dimension standing waves (and wave
functions) will look like go to the following web page. This web
page has animated simulations of the vibration of a drum head.
http://www.kettering.edu/~drussell/Demos/MembraneCircle/Circle.html
To orient yourself have a look at the animations entitled (0,1). This animation is the three-dimensional equivalent of n = 1, as shown above.
The animations (0,2) and (0,3) behave in a similar way to animation (0,1) except they have more nodes. This implies these standing waves have more energy.
You will notice that the animation (1,1) looks like the three-dimensional form of n = 2 above. It is quite similar to the animation (1,2). The two standing waves in (1,1) and (1,2) appear to have the same wavelength and so the same energy, but they look a bit different - why is this?
In three-dimensional standing waves we have to consider angular
variation. This comes from having to conserve angular momentum
in these cases.
Angular momentum = Momentum x Radius.
This requires an additional variable to distinguish the wave functions.
We will use a number called the "angular quantum number" - l (in addition to the quantum number n) when describing wave functions of bound states.
Wave functions with l = 0 are always symmetrical about the middle point. Others l = 1 etc. have different symmetries.
In addition moving electrons have magnetic properties depending on the direction of the angular momentum vector. We label the magnetic property of an electron using the "magnetic quantum number" - m.